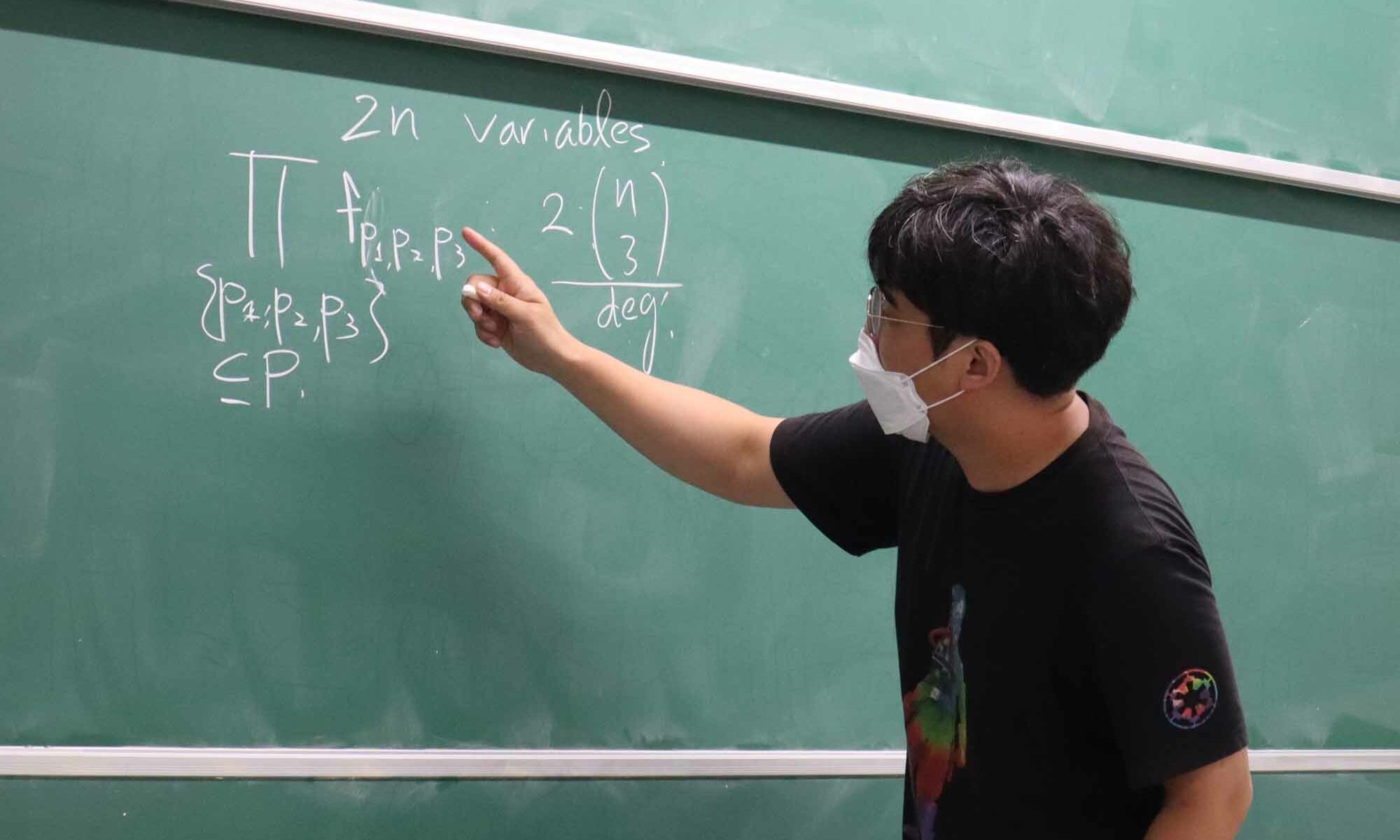Tag: 이승훈

Given a hypergraph $H=(V,E)$, we say that $H$ is (weakly) $m$-colorable if there is a coloring $c:V\to [m]$ such that every hyperedge of $H$ is not monochromatic. The (weak) chromatic number of $H$, denoted by $\chi(H)$, is the smallest $m$ such that $H$ is $m$-colorable. A vertex subset $T \subseteq V$ is called a transversal of $H$ if for every hyperedge $e$ of $H$ we have $T\cap e \ne \emptyset$. The transversal number of $H$, denoted by $\tau(H)$, is the smallest size of a transversal in $H$. The transversal ratio of $H$ is the quantity $\tau(H)/|V|$ which is between 0 and 1. Since a lower bound on the transversal ratio of $H$ gives a lower bound on $\chi(H)$, these two quantities are closely related to each other.

Upon my previous presentation, which is based on the joint work with Joseph Briggs and Michael Gene Dobbins (https://www.youtube.com/watch?v=WLY-8smtlGQ), we update what is discovered in the meantime about transversals and colororings of geometric hypergraphs. In particular, we focus on chromatic numbers of $k$-uniform hypergraphs which are embeddable in $\mathbb{R}^d$ by varying $k$, $d$, and the notion of embeddability and present lower bound constructions. This result can also be regarded as an improvement upon the research program initiated by Heise, Panagiotou, Pikhurko, and Taraz, and the program by Lutz and Möller. We also present how this result is related to the previous results and open problems regarding transversal ratios. This presentation is based on the joint work with Eran Nevo.

We call an order type inscribable if it is realized by a point configuration where all extreme points are all on a circle. In this talk, we investigate inscribability of order types. We first show that every simple order type with at most 2 interior points is inscribable, and that the number of such order types is $\Theta(\frac{4^n}{n^{3/2}})$. We further construct an infinite family of minimally uninscribable order types. The proof of uninscribability mainly uses Möbius transformations. We also suggest open problems around inscribability. This is a joint work with Michael Gene Dobbins.

Motivated from the surrounding property of a point set in $\mathbb{R}^d$ introduced by Holmsen, Pach and Tverberg, we consider the transversal number and chromatic number of a simplicial sphere. As an attempt to give a lower bound for the maximum transversal ratio of simplicial $d$-spheres, we provide two infinite constructions. The first construction gives infinitely many $(d+1)$-dimensional simplicial polytopes with the transversal ratio exactly $\frac{2}{d+2}$ for every $d\geq 2$. In the case of $d=2$, this meets the previously well-known upper bound $1/2$ tightly. The second gives infinitely many simplicial 3-spheres with the transversal ratio greater than $1/2$. This was unexpected from what was previously known about the surrounding property. Moreover, we show that, for $d\geq 3$, the facet hypergraph $\mathcal{F}(\mathbf{P})$ of a $(d+1)$-dimensional simplicial polytope $\mathbf{P}$ has the chromatic number $\chi(\mathcal{F}(\mathbf{P})) \in O(n^{\frac{\lceil d/2\rceil-1}{d}})$, where $n$ is the number of vertices of $\mathbf{P}$. This slightly improves the upper bound previously obtained by Heise, Panagiotou, Pikhurko, and Taraz. This is a joint work with Joseph Briggs and Michael Gene Dobbins.

Given a graph $G$ on the vertex set $V$, the non-matching complex of $G$, $\mathsf{NM}_k(G)$, is the family of subgraphs $G’ \subset G$ whose matching number $\nu(G’)$ is strictly less than $k$. As an attempt to generalize the result by Linusson, Shareshian and Welker on the homotopy types of $\mathsf{NM}_k(K_n)$ and $\mathsf{NM}_k(K_{r,s})$ to arbitrary graphs $G$, we show that (i) $\mathsf{NM}_k(G)$ is $(3k-3)$-Leray, and (ii) if $G$ is bipartite, then $\mathsf{NM}_k(G)$ is $(2k-2)$-Leray. This result is obtained by analyzing the homology of the links of non-empty faces of the complex $\mathsf{NM}_k(G)$, which vanishes in all dimensions $d\geq 3k-4$, and all dimensions $d \geq 2k-3$ when $G$ is bipartite. As a corollary, we have the following rainbow matching theorem which generalizes the result by Aharoni et. al. and Drisko’s theorem: Let $E_1, \dots, E_{3k-2}$ be non-empty edge subsets of a graph and suppose that $\nu(E_i\cup E_j)\geq k$ for every $i\ne j$. Then $E=\bigcup E_i$ has a rainbow matching of size $k$. Furthermore, the number of edge sets $E_i$ can be reduced to $2k-1$ when $E$ is the edge set of a bipartite graph.

This is a joint work with Andreas Holmsen.