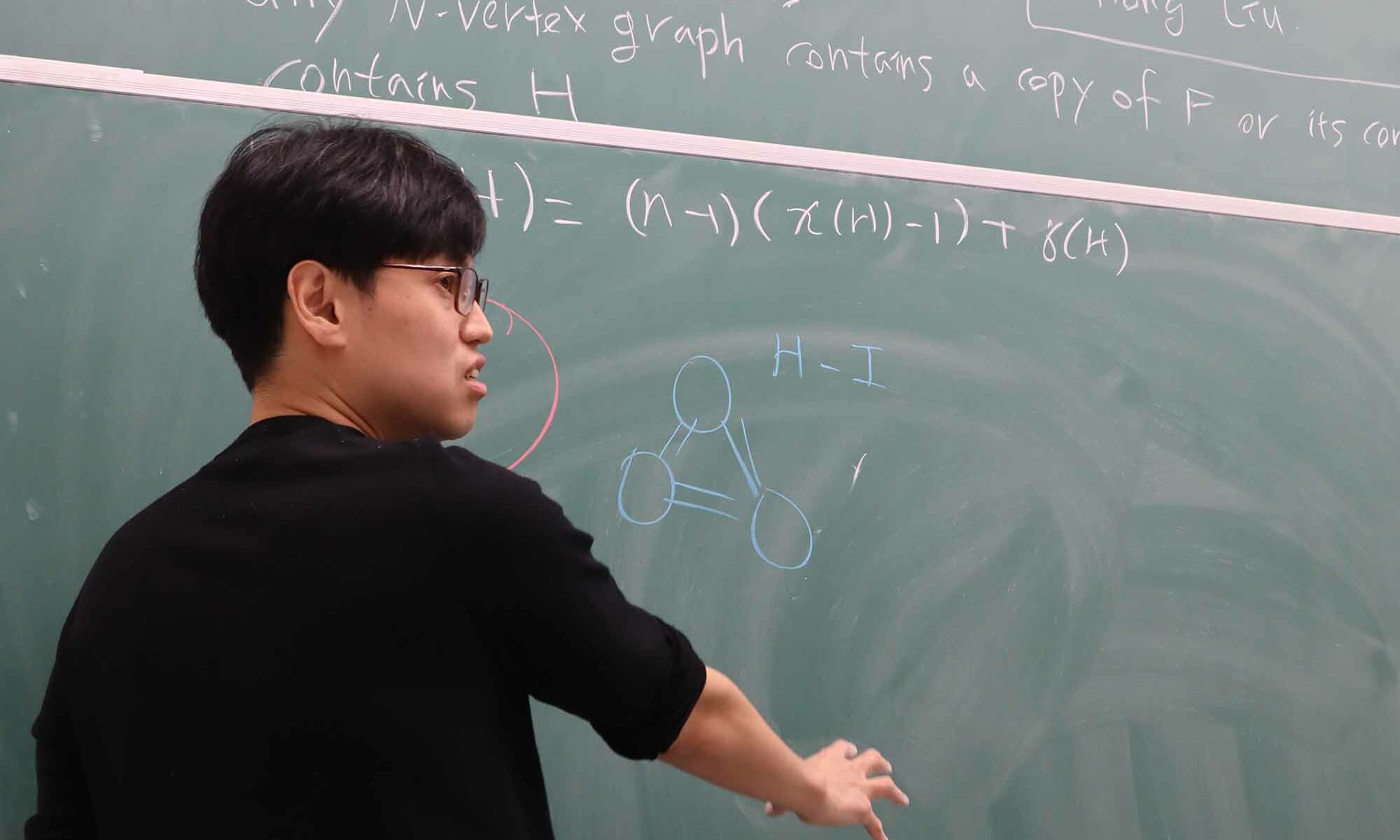On March 21, 2022, Jaehoon Kim (김재훈) from KAIST gave a talk at the Discrete Math Seminar on the Ramsey number with respect to a cycle graph and an arbitrary graph. The title of his talk was “Ramsey numbers of cycles versus general graphs“.
Jaehoon Kim (김재훈), Ramsey numbers of cycles versus general graphs
The Ramsey number $R(F,H)$ is the minimum number $N$ such that any $N$-vertex graph either contains a copy of $F$ or its complement contains $H$. Burr in 1981 proved a pleasingly general result that for any graph $H$, provided $n$ is sufficiently large, a natural lower bound construction gives the correct Ramsey number involving cycles: $R(C_n,H)=(n-1)(\chi(H)-1)+\sigma(H)$, where $\sigma(H)$ is the minimum possible size of a colour class in a $\chi(H)$-colouring of $H$. Allen, Brightwell and Skokan conjectured that the same should be true already when $n\geq |H|\chi(H)$.
We improve this 40-year-old result of Burr by giving quantitative bounds of the form $n\geq C|H|\log^4\chi(H)$, which is optimal up to the logarithmic factor. In particular, this proves a strengthening of the Allen-Brightwell-Skokan conjecture for all graphs $H$ with large chromatic number.
This is joint work with John Haslegrave, Joseph Hyde and Hong Liu
Jaehoon Kim (김재훈) gave a talk on a sufficient condition for a 2-complex to have a unique embedding in a 3-dimensional space, which is a 3-dimensional analog of Whitney’s theorem on the uniqueness of planar embeddings of a 3-connected graph at the Discrete Math Seminar
On November 9, 2021, Jaehoon Kim (김재훈) from KAIST gave a talk at the Discrete Math Seminar on a 3-dimensional analog of Whitney’s theorem on the uniqueness of planar embeddings of a 3-connected graph. The title of his talk was “2-complexes with unique embeddings in 3-space“.
Jaehoon Kim (김재훈), 2-complexes with unique embeddings in 3-space
A well-known theorem of Whitney states that a 3-connected planar graph admits an essentially unique embedding into the 2-sphere. We prove a 3-dimensional analogue: a simply-connected 2-complex every link graph of which is 3-connected admits an essentially unique locally flat embedding into the 3-sphere, if it admits one at all. This can be thought of as a generalisation of the 3-dimensional Schoenflies theorem. This is joint work with Agelos Georgakopoulos.
Jaehoon Kim (김재훈) gave a talk on the minimum spectral radius of $K_{r+1}$-saturated graphs at the Discrete Math Seminar
On July 13, 2021, Jaehoon Kim (김재훈) from KAIST gave a talk at the Discrete Math Seminar on a lower bound on the spectral radius of a $K_{r+1}$-saturated graph. The title of his talk was “$K_{r+1}$-saturated graphs with small spectral radius“.
Jaehoon Kim (김재훈), $K_{r+1}$-saturated graphs with small spectral radius
For a graph $H$, a graph $G$ is $H$-saturated if $G$ does not contain $H$ as a subgraph but for any $e\in E(\overline G)$, $G+e$ contains $H$. In this note, we prove a sharp lower bound for the number of paths and walks on length 2 in $n$-vertex $K_{r+1}$-saturated graphs. We then use this bound to give a lower bound on the spectral radii of such graphs which is asymptotically tight for each fixed $r$ and $n\to \infty$.
Extremal and Probabilistic Combinatorics (2021 KMS Spring Meeting)
A special session “Extremal and Probabilistic Combinatorics” at the 2021 KMS Spring Meeting is organized by Tuan Tran.
URL: https://www.kms.or.kr/meetings/spring2021/
Speakers and Schedule
All talks are on April 30.
- [9:00 am] Joonkyung Lee (이준경), University College London
- Majority dynamics on sparse random graphs
- [9:30 am] Dong Yeap Kang (강동엽), Unversity of Birmingham
- The Erdős-Faber-Lovász conjecture and related results
- [10:00 am] Jinyoung Park (박진영), IAS
- The threshold for the square of a Hamilton cycle
- [10:50 am] Debsoumya Chakraborti, IBS Discrete Mathematics Group
- Generalized graph saturation
- [11:20 am] Jaehoon Kim (김재훈), KAIST
- Resolution of the Oberwolfach problem
- [11:50 am] Hong Liu, University of Warwick
- Sublinear expanders and its applications
Abstracts
Debsoumya Chakraborti, Generalized graph saturation
Graph saturation is one of the oldest areas of investigation in extremal combinatorics. A graph G is called F-saturated if G does not contain a subgraph isomorphic to F, but the addition of any edge creates a copy of F. We resolve one of the most fundamental questions of minimizing the number of cliques of size r in a $K_s$-saturated graph for all sufficiently large numbers of vertices, confirming a conjecture of Kritschgau, Methuku, Tait and Timmons. We further prove a corresponding stability result. This talk will be based on joint work with Po-Shen Loh.
Jaehoon Kim (김재훈), Resolution of the Oberwolfach problem
The Oberwolfach problem, posed by Ringel in 1967, asks for a decomposition of $K_{2n+1}$ into edge-disjoint copies of a given 2-factor. We show that this can be achieved for all large n. We actually prove a significantly more general result, which allows for decompositions into more general types of factors.
Dong Yeap Kang (강동엽), The Erdős-Faber-Lovász conjecture and related results
A hypergraph is linear if every pair of two distinct edges shares at most one vertex. A longstanding conjecture by Erdős, Faber, and Lovász in 1972, states that the chromatic index of any linear hypergraph on n vertices is at most n.
In this talk, I will present the ideas to prove the conjecture for all large n. This is joint work with Tom Kelly, Daniela Kühn, Abhishek Methuku, and Deryk Osthus.
Joonkyung Lee (이준경), Majority dynamics on sparse random graphs
Majority dynamics on a graph G is a deterministic process such that every vertex updates its {-1,1}-assignment according to the majority assignment on its neighbor simultaneously at each step. Benjamini, Chan, O’Donnell, Tamuz and Tan conjectured that, in the Erdős-Rényi random graph G(n,p), the random initial {-1,1}-assignment converges to the unanimity with high probability whenever p>> 1/n.
This conjecture was firstly confirmed for $p>Cn^{-1/2}$ for a large constant C>0 by Fountoulakis, Kang and Makai. Although this result has been reproved recently by Tran and Vu and by Berkowitz and Devlin, none of them managed to extend it beyond the barrier $p>Cn^{-1/2}$. We prove the conjecture for sparser random graphs G(n,p), where $Dn^{-3/5}\log n < p < C n^{-1/2}$ with a large constant D>0.
Joint work with Debsoumya Chakraborti, Jeong Han Kim and Tuan Tran.
Hong Liu, Sublinear expanders and its applications
I will review the history of sublinear expander and present some recent applications, which lead to resolutions of several long-standing problems in sparse graphs embeddings.
Jinyoung Park (박진영), The threshold for the square of a Hamilton cycle
We will talk about a recent result of Jeff Kahn, Bhargav Narayanan, and myself stating that the threshold for the random graph G(n,p) to contain the square of a Hamilton cycle is $1/\sqrt n$, resolving a conjecture of Kühn and Osthus from 2012. The proof idea is motivated by the recent work of Frankston and the three aforementioned authors on a conjecture of Talagrand — “a fractional version of Kahn-Kalai expectation threshold conjecture.”
Jaehoon Kim (김재훈) gave a talk on a resilience version of Pósa’s theorem regarding Hamiltonian cycles at the Discrete Math Seminar
On June 23, 2020, Jaehoon Kim (김재훈) from KAIST presented his work with Padraig Condon, Alberto Espuny Diaz, Daniela Kühn and Deryk Osthus on a resilience version of Pósa’s theorem regarding a sufficient condition on the degree sequence for a graph to have a Hamiltonian cycle at the Discrete Math Seminar. The title of his talk is “A resilience version of Pósa’s theorem“.
Jaehoon Kim (김재훈), A resilience version of Pósa’s theorem
Pósa’s theorem states that any graph G whose degree sequence $d_1\leq \dots \leq d_n$ satisfies $d_i \geq i+1$ for all $i< n/2$ has a Hamilton cycle. This degree condition is best possible. We show that a similar result holds for suitable subgraphs $G$ of random graphs. This is joint work with Padraig Condon, Alberto Espuny Diaz, Daniela Kühn and Deryk Osthus.
“2019 Combinatorics Workshop” was held from August 13 to August 15, 2019 at Incheon.

The 2019 Combinatorics Workshop (2019 조합론 학술대회) was held from August 13, 2019 to August 15, 2019 at the SKYPARK Hotel, Songdo, Incheon. There were 16 talks.
Plenary Speaker
- Mihyun Kang (강미현), Graz University of Technology
Keynote Speakers
- Jaehoon Kim (김재훈), KAIST
- Seung Jin Lee (이승진), Seoul National University
- Meesue Yoo (유미수), Dankook University
Invited Speakers
- Eun-Kyung Cho (조은경), Hankuk University of Foreign Studies
- Soogang Eoh (어수강), Seoul National University
- JiSun Huh (허지선), Sungkyunkwan University
- Jihyeug Jang (장지혁), Sungkyunkwan University
- Dong Yeap Kang (강동엽), KAIST and IBS Discrete Mathematics Group
- Min Jeong Kang (강민정), Incheon National University
- Dabeen Lee (이다빈), IBS Discrete Mathematics Group
- Kang-Ju Lee (이강주), Seoul National University
- Myeonghwan Lee (이명환), Incheon National University
- Jihye Park (박지혜), Yeungnam University
- Sun-mi Yun (윤선미), Sungkyunkwan University