기초과학연구원 이산수학그룹
On September 2, 2025, Zhifei Yan from the IBS Extremal Combinatorics and Probability Group gave a talk at the Discrete Math Seminar on covering the vertex set of a properly edge-colored graph with two vertex-disjoint rainbow cycles. The title of his talk was “A Rainbow version of Lehel’s conjecture“.
The IBS discrete mathematics group welcomes Dr. Zhifei Yan, a new research fellow at the IBS Extremal Combinatorics and Probability Group, starting September 1, 2025. He received his Ph.D. in 2025 from the Instituto Nacional de Matemática Pura e Aplicada (IMPA), Rio de Janeiro, Brazil, under the supervision of Prof. Rob Morris. He is interested in extremal and probabilistic combinatorics.
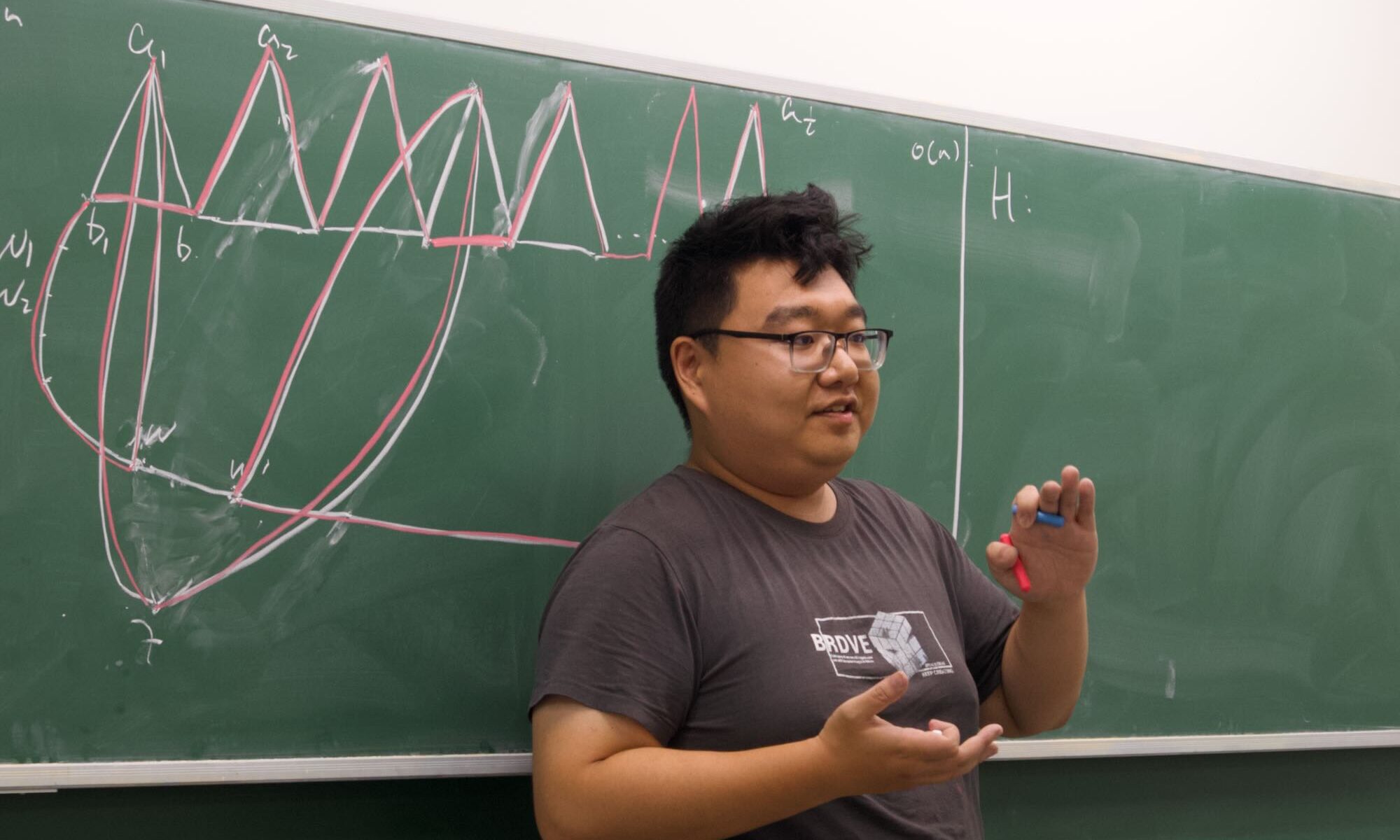
Lehel’s conjecture states that every 2-edge-colouring of the complete graph $K_n$ admits a partition of its vertices into two monochromatic cycles. This was proven for sufficiently large n by Luczak, Rödl, and Szemerédi (1998), extended by Allen (2008), and fully resolved by Bessy and Thomassé in 2010.
We consider a rainbow version of Lehel’s conjecture for properly edge-coloured complete graphs. We prove that for any properly edge-coloured $K_n$ with sufficiently large n, there exists a partition of the vertex set into two rainbow cycles, each containing no two edges of the same colour.
This is joint work with Pedro Araújo, Xiaochuan Liu, Taísa Martins, Walner Mendonça, Luiz Moreira, and Vinicius Fernandes dos Santos.