Tag: SebastianWiederrecht

We prove the existence of a computable function $f\colon\mathbb{N}\to\mathbb{N}$ such that for every integer $k$ and every digraph $D$ either contains a collection $\mathcal{C}$ of $k$ directed cycles of even length such that no vertex of $D$ belongs to more than four cycles in $\mathcal{C}$, or there exists a set $S\subseteq V(D)$ of size at most $f(k)$ such that $D-S$ has no directed cycle of even length.

This is joint work with Maximilian Gorsky, Ken-ichi Kawarabayashi, and Stephan Kreutzer.

In 1986, Robertson and Seymour proved a generalization of the seminal result of Erdős and Pósa on the duality of packing and covering cycles: A graph has the Erdős-Pósa property for minor if and only if it is planar. In particular, for every non-planar graph $H$ they gave examples showing that the Erdős-Pósa property does not hold for $H$. Recently, Liu confirmed a conjecture of Thomas and showed that every graph has the half-integral Erdős-Pósa property for minors.

In this talk, we start the delineation of the half-integrality of the Erdős-Pósa property for minors. We conjecture that for every graph $H$ there exists a finite family $\mathfrak{F}_H$ of parametric graphs such that $H$ has the Erdős-Pósa property in a minor-closed graph class $\mathcal{G}$ if and only if $\mathcal{G}$ excludes a minor of each of the parametric graphs in $\mathfrak{F}_H$. We prove this conjecture for the class $\mathcal{H}$ of Kuratowski-connected shallow-vortex minors by showing that, for every non-planar $H\in\mathcal{H}$ the family $\mathfrak{F}_H$ can be chosen to be precisely the two families of Robertson-Seymour counterexamples to the Erdős-Pósa property of $H$.

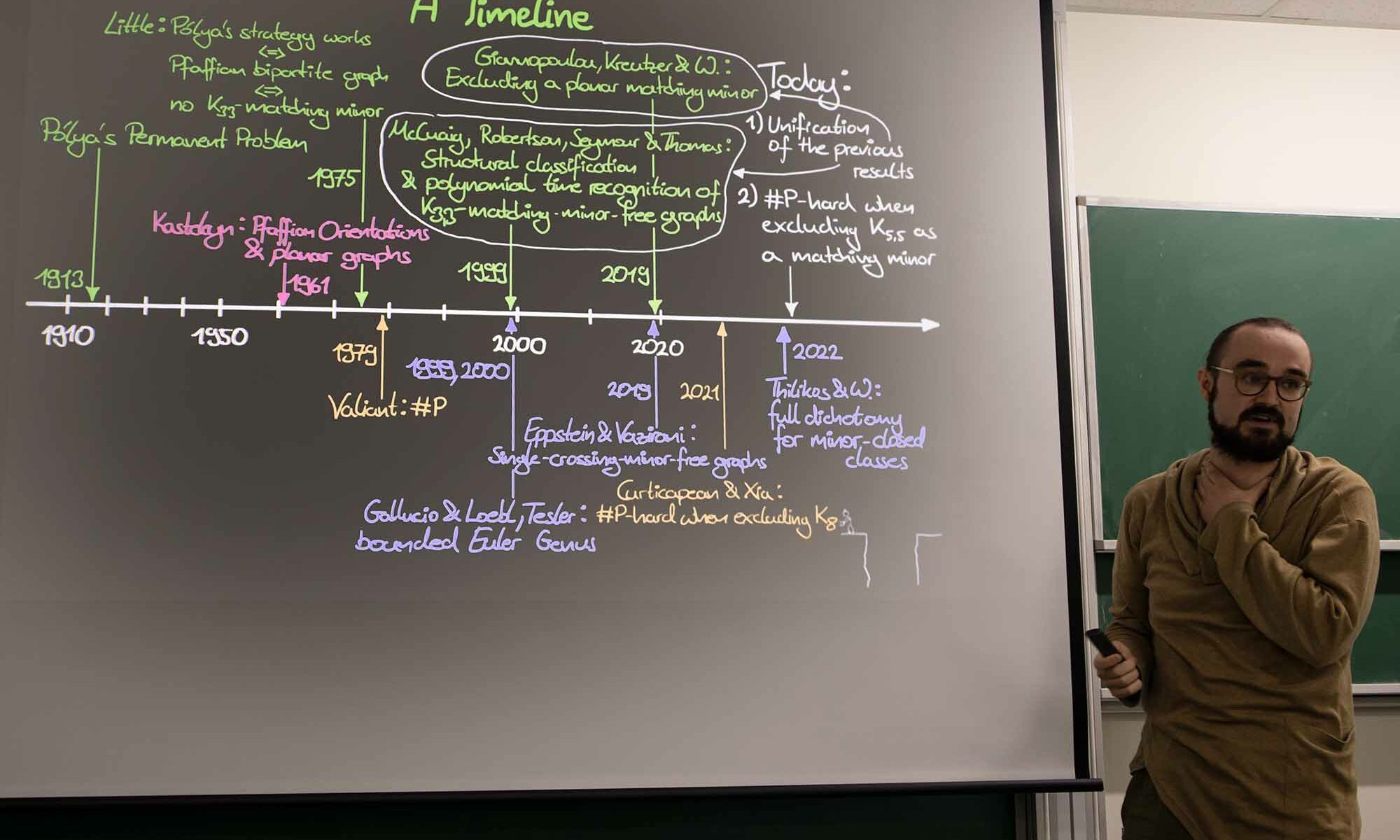
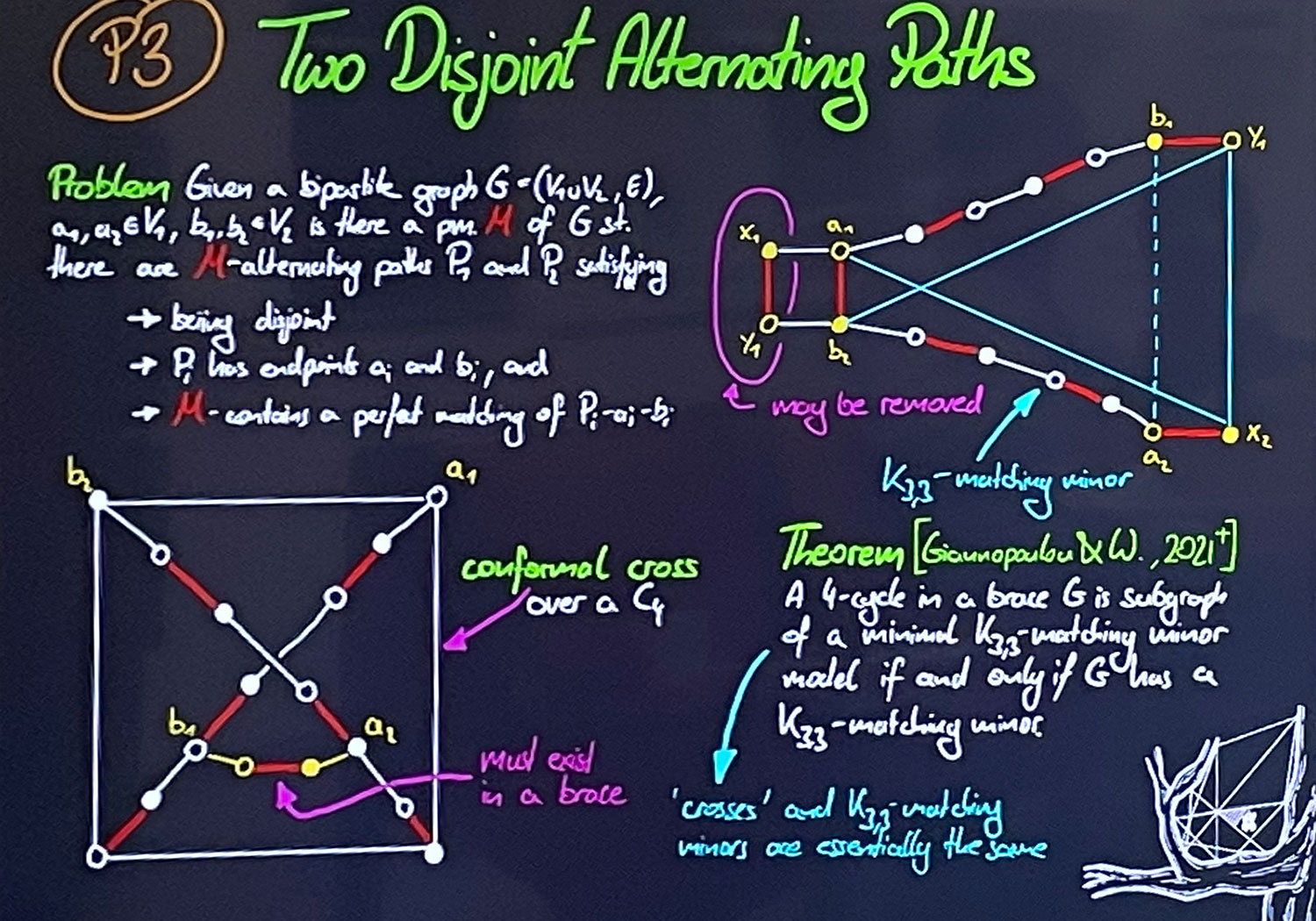
By a seminal result of Valiant, computing the permanent of (0, 1)-matrices is, in general, #P-hard. In 1913 Pólya asked for which (0, 1)-matrices A it is possible to change some signs such that the permanent of A equals the determinant of the resulting matrix. In 1975, Little showed these matrices to be exactly the biadjacency matrices of bipartite graphs excluding $K_{3,3}$ as a matching minor. This was turned into a polynomial time algorithm by McCuaig, Robertson, Seymour, and Thomas in 1999. However, the relation between the exclusion of some matching minor in a bipartite graph and the tractability of the permanent extends beyond K3,3. Recently it was shown that the exclusion of any planar bipartite graph as a matching minor yields a class of bipartite graphs on which the permanent of the corresponding (0, 1)-matrices can be computed efficiently.

In this paper we unify the two results above into a single, more general result in the style of the celebrated structure theorem for single-crossing minor-free graphs. We identify a class of bipartite graphs strictly generalising planar bipartite graphs and $K_{3,3}$ which includes infinitely many non-Pfaffian graphs. The exclusion of any member of this class as a matching minor yields a structure that allows for the efficient evaluation of the permanent. Moreover, we show that the evaluation of the permanent remains #P-hard on bipartite graphs which exclude $K_{5,5}$ as a matching minor. This establishes a first computational lower bound for the problem of counting perfect matchings on matching minor closed classes. As another application of our structure theorem, we obtain a strict generalisation of the algorithm for the k-vertex disjoint directed paths problem on digraphs of bounded directed treewidth.

This is joint work with Archontia Giannopoulou and Dimitrios Thilikos.

The Structural Theorem of the Graph Minors series of Robertson and Seymour asserts that, for every $t\in\mathbb{N},$ there exists some constant $c_{t}$ such that every $K_{t}$-minor-free graph admits a tree decomposition whose torsos can be transformed, by the removal of at most $c_{t}$ vertices, to graphs that can be seen as the union of some graph that is embeddable to some surface of Euler genus at most $c_{t}$ and “at most $c_{t}$ vortices of depth $c_{t}$”. Our main combinatorial result is a “vortex-free” refinement of the above structural theorem as follows: we identify a (parameterized) graph $H_{t}$, called shallow vortex grid, and we prove that if in the above structural theorem we replace $K_{t}$ by $H_{t},$ then the resulting decomposition becomes “vortex-free”. Up to now, the most general classes of graphs admitting such a result were either bounded Euler genus graphs or the so called single-crossing minor-free graphs. Our result is tight in the sense that, whenever we minor-exclude a graph that is not a minor of some $H_{t},$ the appearance of vortices is unavoidable. Using the above decomposition theorem, we design an algorithm that, given an $H_{t}$-minor-free graph $G$, computes the generating function of all perfect matchings of $G$ in polynomial time. This algorithm yields, on $H_{t}$-minor-free graphs, polynomial algorithms for computational problems such as the {dimer problem, the exact matching problem}, and the computation of the permanent. Our results, combined with known complexity results, imply a complete characterization of minor-closed graphs classes where the number of perfect matchings is polynomially computable: They are exactly those graph classes that do not contain every $H_{t}$ as a minor. This provides a sharp complexity dichotomy for the problem of counting perfect matchings in minor-closed classes.

This is joint work with Dimitrios M. Thilikos.