기초과학연구원 이산수학그룹
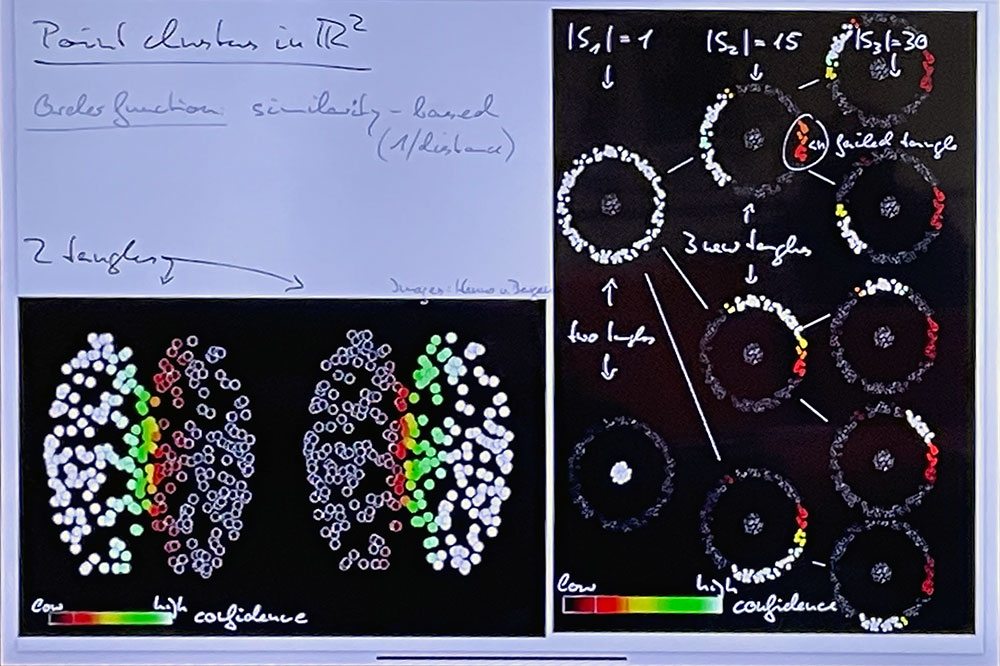
On April 21, 2021, Reinhard Diestel from the University of Hamburg gave an online talk at the Virtual Discrete Math Colloquium about the abstract tangle theory and its applications to real-world examples such as clustering. The title of his talk was “Tangles of set separations: a novel clustering method and type recognition in machine learning“.
Traditional clustering identifies groups of objects that share certain qualities. Tangles do the converse: they identify groups of qualities that typically occur together. They can thereby discover, relate, and structure types: of behaviour, political views, texts, or proteins. Tangles offer a new, quantitative, paradigm for grouping phenomena rather than things. They can identify key phenomena that allow predictions of others. Tangles also offer a new paradigm for clustering in large data sets.
The mathematical theory of tangles has its origins in the theory of graph minors developed by Robertson and Seymour. It has recently been axiomatized in a way that makes it applicable to a wide range of contexts outside mathematics: from clustering in data science to predicting customer behaviour in economics, from DNA sequencing and drug development to text analysis and machine learning.
This very informal talk will not show you the latest intricacies of abstract tangle theory (for which you can find links on the tangle pages of my website), but to win you over to join our drive to develop real tangle applications in areas as indicated above. We have some software to share, but are looking for people to try it out with us on real-world examples!
Here are some introductory pages from a book I am writing on this, which may serve as an extended abstract: https://arxiv.org/abs/2006.01830