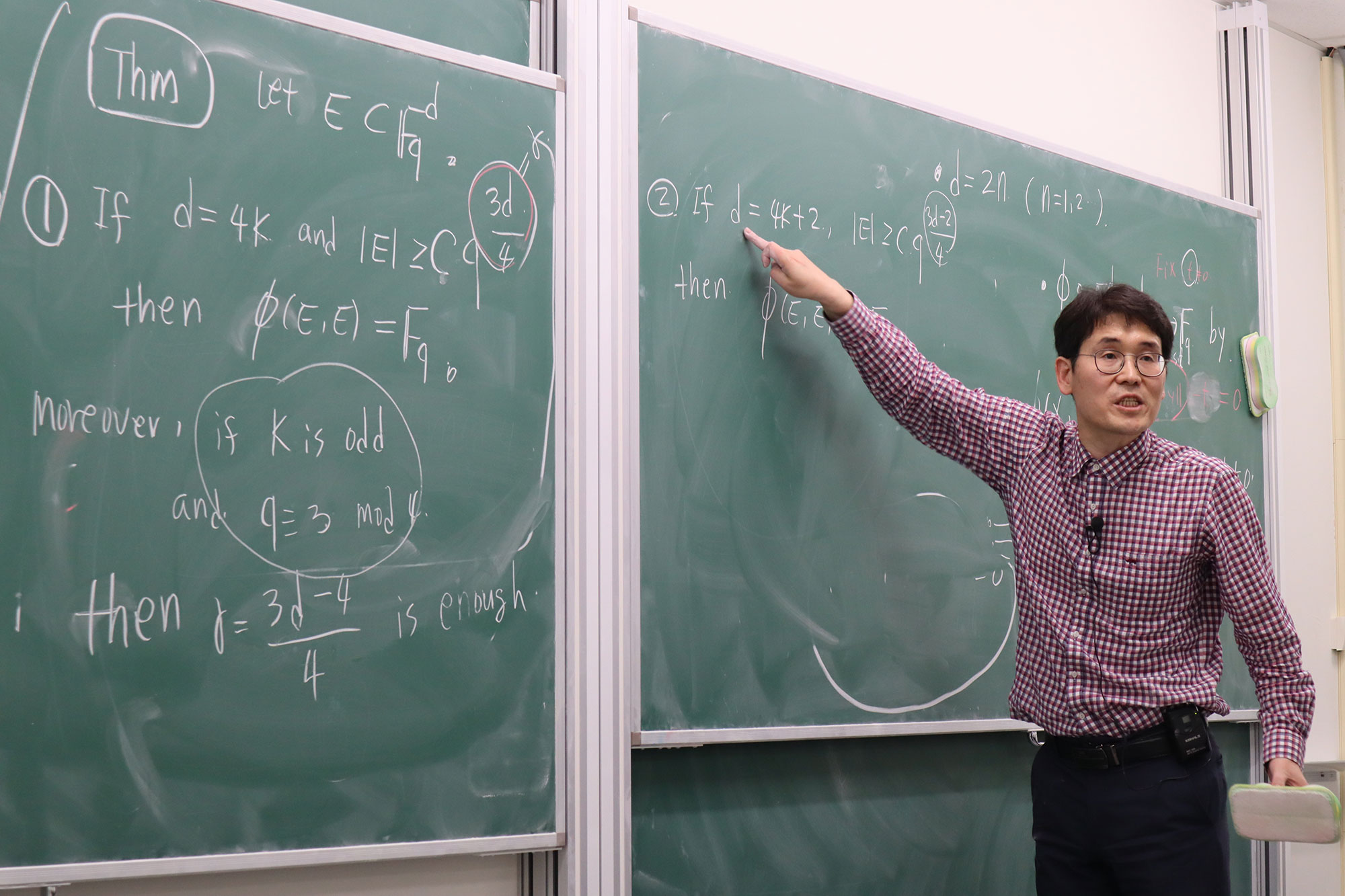On June 1, 2021, Doowon Koh (고두원) from Chungbuk National University gave a talk on a variation of the Erdős–Falconer distinct distance problem over finite fields at the Discrete Math Seminar. The title of the talk was “Mattila-Sjölin type functions: A finite field model“.
Doowon Koh (고두원), Mattila-Sjölin type functions: A finite field model
Let $\mathbb{F}_q$ be a finite field of order $q$ which is a prime power. In the finite field setting, we say that a function $\phi\colon \mathbb{F}_q^d\times \mathbb{F}_q^d\to \mathbb{F}_q$ is a Mattila-Sjölin type function in $\mathbb{F}_q^d$ if for any $E\subset \mathbb{F}_q^d$ with $|E|\gg q^{\frac{d}{2}}$, we have $\phi(E, E)=\mathbb{F}_q$. The main purpose of this talk is to present the existence of such a function. More precisely, we will construct a concrete function $\phi: \mathbb{F}_q^4\times \mathbb{F}_q^4\to \mathbb{F}_q$ with $q\equiv 3 \mod{4}$ such that if $E\subset \mathbb F_q^4$ with $|E|>q^2,$ then $\phi(E,E)=\mathbb F_q$. This is a joint work with Daewoong Cheong, Thang Pham, and Chun-Yen Shen.
Doowon Koh (고두원) gave a talk on the approach to an upper bound of the point-sphere incidences over the finite field from the restriction estimates for cones at the Discrete Math Seminar
On February 9, 2021, Doowon Koh (고두원) from Chungbuk National University gave a talk at the Discrete Math Seminar on the restriction conjecture for the cone in four dimensions and its applications to the upper bound on the point-sphere incidences in the field field setting. The title of his talk was “On the cone restriction conjecture in four dimensions and applications in incidence geometry“.
Doowon Koh (고두원), On the cone restriction conjecture in four dimensions and applications in incidence geometry
Main purpose of this talk is to introduce a connection between restriction estimates for cones and point-sphere incidence theorems in the finite field setting. First, we review the finite field restriction problem for cones and address new results on the conical restriction problems. In particular, we establish the restriction conjecture for the cone in four dimensions. Second, we study how to apply the conical restriction results to the point-sphere incidence bounds. As a consequence, we obtain sharp point-sphere incidence bounds when sphere sets are not too big.