Tag: SzymonToruńczyk

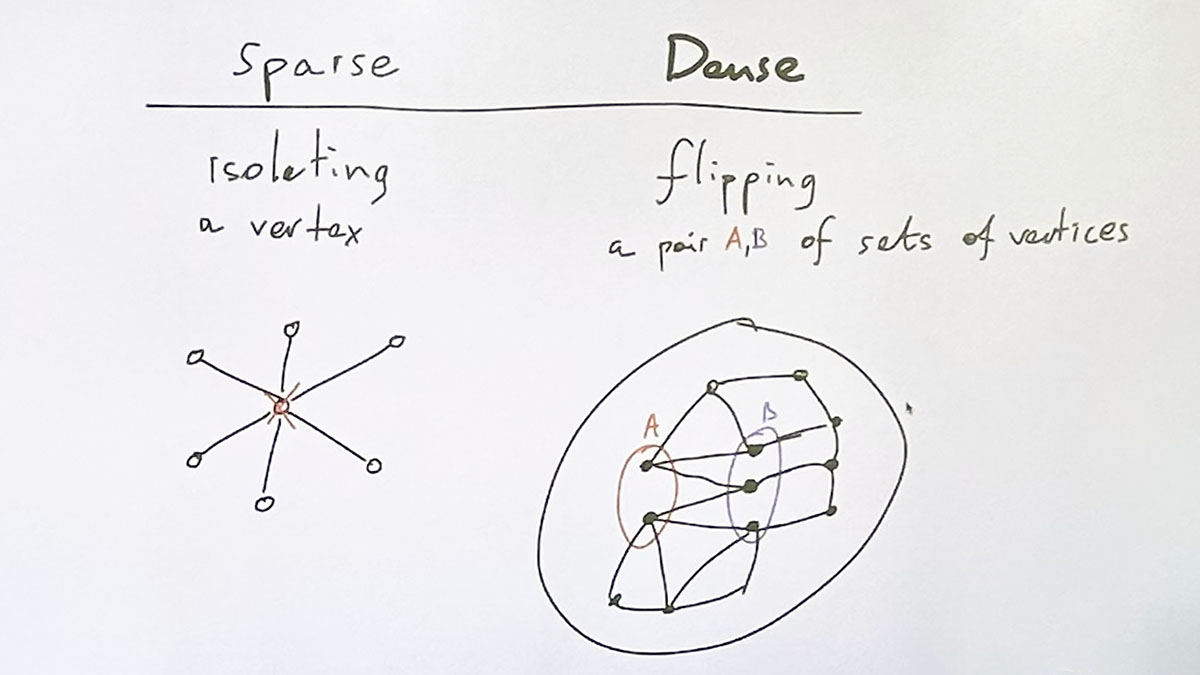
We define new graph parameters, called flip-width, that generalize treewidth, degeneracy, and generalized coloring numbers for sparse graphs, and clique-width and twin-width for dense graphs. The flip-width parameters are defined using variants of the Cops and Robber game, in which the robber has speed bounded by a fixed constant r∈N∪{∞}, and the cops perform flips (or perturbations) of the considered graph. We then propose a new notion of tameness of a graph class, called bounded flip-width, which is a dense counterpart of classes of bounded expansion of Nešetril and Ossona de Mendez, and includes classes of bounded twin-width of Bonnet, Kim, Thomassé, and Watrigant. This unifies Sparsity Theory and Twin-width Theory, providing a common language for studying the central notions of the two theories, such as weak coloring numbers and twin-width — corresponding to winning strategies of one player — or dense shallow minors, rich divisions, or well-linked sets, corresponding to winning strategies of the other player. We prove that boundedness of flip-width is preserved by first-order interpretations, or transductions, generalizing previous results concerning classes of bounded expansion and bounded twin-width. We provide an algorithm approximating the flip-width of a given graph, which runs in slicewise polynomial time (XP) in the size of the graph. Finally, we propose a more general notion of tameness, called almost bounded flip-width, which is a dense counterpart of nowhere dense classes. We conjecture, and provide evidence, that classes with almost bounded flip-width coincide with monadically dependent (or monadically NIP) classes, introduced by Shelah in model theory. We also provide evidence that classes of almost bounded flip-width characterise the hereditary graph classes for which the model-checking problem is fixed-parameter tractable.