On March 10, 2022, Fedor Fomin from the University of Bergen gave an online talk at the Virtual Discrete Math Colloquium on the parameterized complexity of determining whether a 2-connected graph has a cycle of length at least k plus the bound given by the Dirac’s theorem or the Erdős-Gallai theorem. The title of his talk was “Long cycles in graphs: Extremal Combinatorics meets Parameterized Algorithms“.
Fedor Fomin, Long cycles in graphs: Extremal Combinatorics meets Parameterized Algorithms
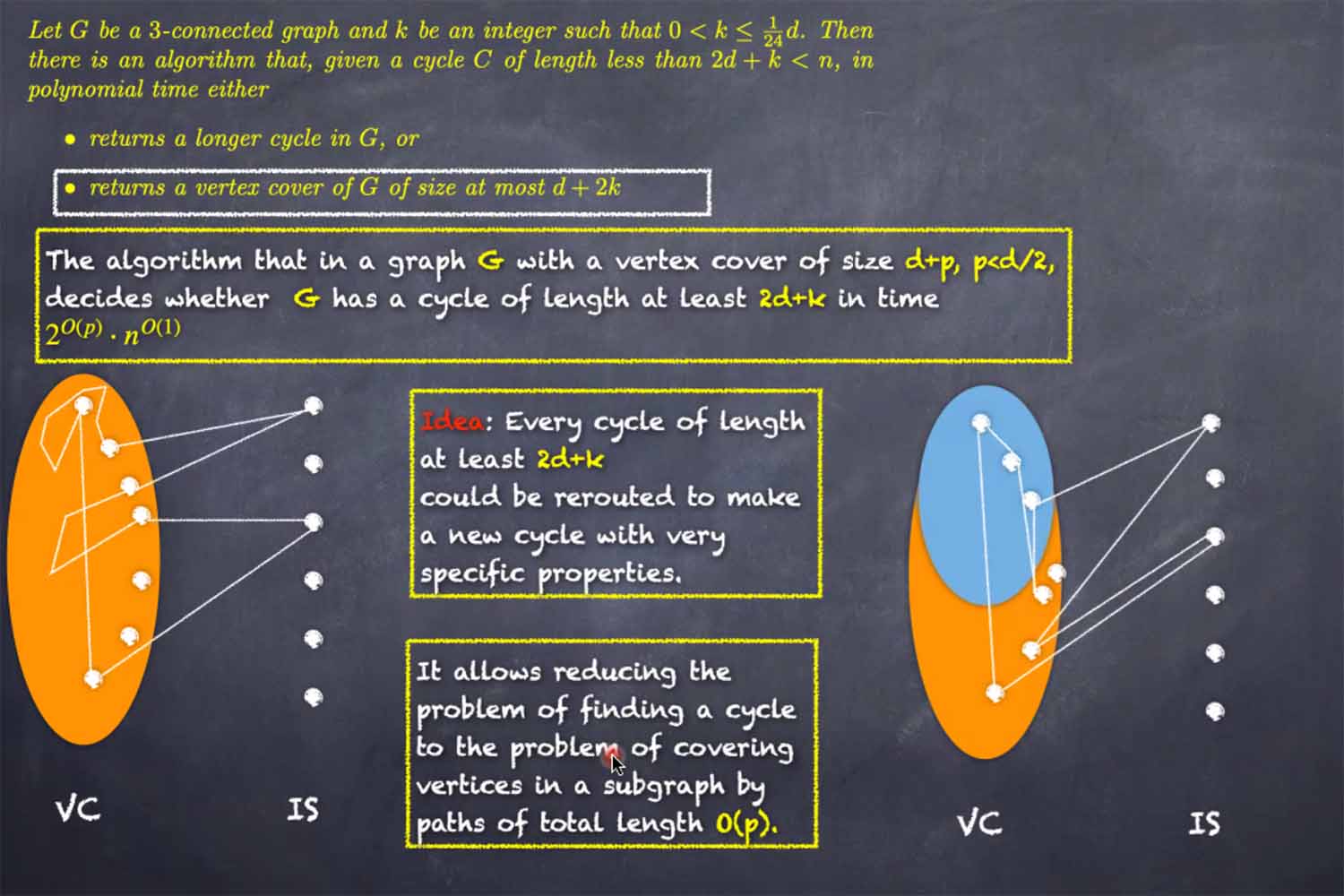
We examine algorithmic extensions of two classic results of extremal combinatorics. First, the theorem of Dirac from 1952 asserts that a 2-connected graph G with the minimum vertex degree d>1, is either Hamiltonian or contains a cycle of length at least 2d. Second, the theorem of Erdős-Gallai from 1959, states that a 2-connected graph G with the average vertex degree D>1, contains a cycle of length at least D.
We discuss the recent progress in parameterized complexity of computing long cycles “above” the guarantees established by these classical theorems: cycles of lengths at least 2d+k and D+k.
The talk is based on the joint works with Petr Golovach, Danil Sagunov, and Kirill Simonov.