기초과학연구원 이산수학그룹
On July 29, 2020, Akanksha Agrawal from Ben-Gurion University of the Negev gave the second talk of the online seminar series called the Virtual Discrete Math Colloquium. The title of her talk was “Polynomial Kernel for Interval Vertex Deletion“.
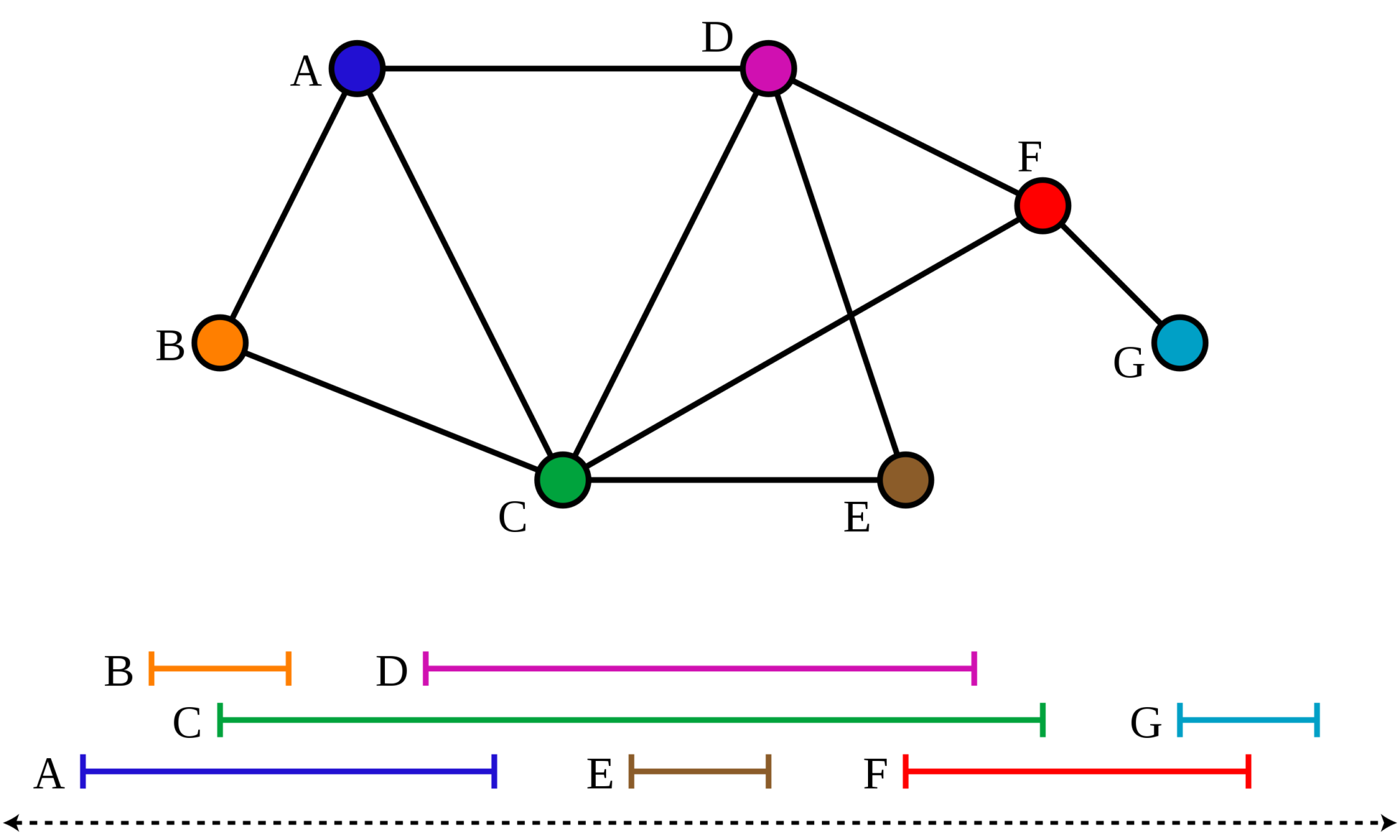
Given a graph G and an integer k, the Interval Vertex Deletion (IVD) problem asks whether there exists a vertex subset S of size at most k, such that G-S is an interval graph. A polynomial kernel for a parameterized problem is a polynomial time preprocessing algorithm that outputs an equivalent instance of the problem whose size is bounded by a polynomial function of the parameter. The existence of a polynomial kernel for IVD remained a well-known open problem in Parameterized Complexity. In this talk we look at a sketch of a polynomial kernel for the problem (with the solution size as the parameter). To illustrate one of the key ingredients of our kernel, we will look at a polynomial kernel for IVD, when parameterized by the vertex cover number.